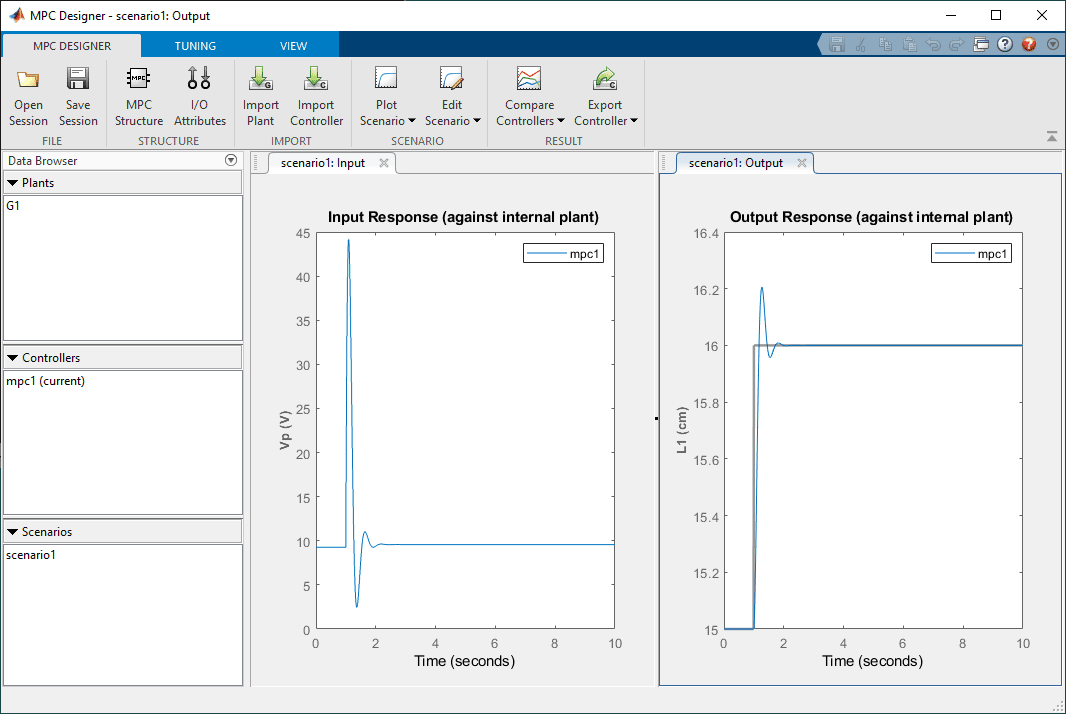
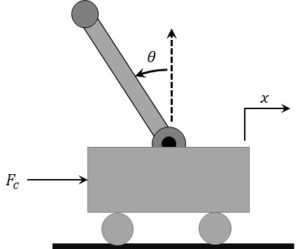
 You would be hard-pressed to find a physics, dynamics, or control system textbook without an example of a pendulum. Why is that? Many students struggle to see how doing work on a seemingly unpractical device will help them learn tools that will be useful in their career or research paths. After all, there are no job postings asking for experience in stabilizing or modeling an inverted pendulum. You don’t see inverted pendulums in real-world devices (or do you?). So why are they used in so many textbooks and found in physics and engineering labs around the world?
You would be hard-pressed to find a physics, dynamics, or control system textbook without an example of a pendulum. Why is that? Many students struggle to see how doing work on a seemingly unpractical device will help them learn tools that will be useful in their career or research paths. After all, there are no job postings asking for experience in stabilizing or modeling an inverted pendulum. You don’t see inverted pendulums in real-world devices (or do you?). So why are they used in so many textbooks and found in physics and engineering labs around the world?
Pendulums are Everywhere
 There are multiple reasons. For one, the inverted pendulum DOES represent many real-world systems. Examples include the Segway, the human posture systems, the launching of a rocket, and so on. Basically, any system that requires vertical stabilization has dynamics that are similar to an inverted pendulum. Sure, the dynamics in these real-world systems are more complex, but they are related. The work involved in modeling and controlling an inverted pendulum carries over to many engineering areas.
There are multiple reasons. For one, the inverted pendulum DOES represent many real-world systems. Examples include the Segway, the human posture systems, the launching of a rocket, and so on. Basically, any system that requires vertical stabilization has dynamics that are similar to an inverted pendulum. Sure, the dynamics in these real-world systems are more complex, but they are related. The work involved in modeling and controlling an inverted pendulum carries over to many engineering areas.
The Ultimate System to Study Modeling and Control Design
Newtonian Physics
The simple hanging pendulum is one of the most common examples to describe periodic motion concepts. Deriving the equation of motion based on Newton’s 2nd Law of Motion and finding the natural frequency (or resonance) of the system is a common exercise.
Lagrangian Mechanics
The Lagrangian method is commonly used to model more complex actuated, two-degree of freedom pendulum configurations such as a rotary or linear inverted pendulum. The Lagrange equations provide a systematic process that is commonly used to derive the nonlinear equations of motions of a pendulum and other complex systems. Learning how to use Lagrange has a huge crossover. They are often used to model systems such as robot manipulators, for instance.
Linearization
The pendulum is often used as a linearization example in dynamic and control systems textbooks. By linearizing the nonlinear equation of motion about an operating point, you can then have a set of linear equations of motion that represents the pendulum for small variations about that point.
State-Space Modeling
Pendulums are often used as an example for state equations. Control engineers commonly use states to describe a system, especially for multiple-input multiple-output (MIMO) systems. Representing the system in linear state-space is especially useful because once in this form, you have many state-feedback control techniques available.
State Feedback Control
That is certainly the case for more advanced pendulum configurations where you have several, multi-variable equations of motion. Typically, the nonlinear equations of motion (EOMs) are derived using the Lagrange method and are linearized about an operating point. The linear equations are used to obtain a linear state-space representation of the system where state-space based control design methods can be used (i.e., “modern control”). Otherwise, if a MIMO system is modeled using transfer functions (i.e., “classic control”), you end up with multiple, separate equations that are more difficult to use when designing a controller for two or more elements, such as controlling the position of the cart while stabilizing an inverted pendulum.
Nonlinear Control
In some cases, the nonlinear model is used to develop nonlinear control algorithms, i.e., not linearizing and designing a linear control. Nonlinear control is more difficult to design, but can lead to better performance, obtain behaviors not possible with linear control, and can be valid over a larger range. One example that Quanser has used for many of its systems is the nonlinear energy-based swing-up control based on the design principles introduced in (Åström & Furuta, 1996).
It’s an Unstable System
Lastly, although this is taken for granted, it should be noted that one of the hallmark features of an inverted pendulum is that it is an unstable system. It is actually very difficult to find nonlinear, unstable systems that you can have in a lab for students and researchers to use. Most of the time, systems are already either stable or marginally stable, and the controller is designed to make the system behave a certain way, e.g., designing a PID controller for a DC motor to control its position to a given command. Stability analysis of unstable systems is a huge part of control engineering. Demonstrating what it means to have a pole in the right-hand plane or studying its Lyapunov function or phase portrait are important principles.
Common – and not so Common Pendulum Configurations
In my next blog post, I will highlight some common and not so common pendulum configurations – from linear and rotary pendulum to Pendubot, Acrobot, and Reaction Wheel Pendulum. Each can be used in a different way and has its own advantages and disadvantages. However, the “advantages” and “disadvantages” are subjective. It really depends on what your goal is. If you want something very difficult to control, then a triple inverted pendulum or the Acrobot might suit you. If you are more interested in using the pendulum as a modeling example, then the classic linear inverted pendulum (cart and pole) might be a better option to avoid the more cumbersome dynamics of rotary-based pendulums. But more on that shortly!
In the meantime, download our free Experience Controls textbook app to learn more about the pendulum modeling methods and control of an inverted pendulum. You can download the Experience Controls app on the App Store or Google Play.