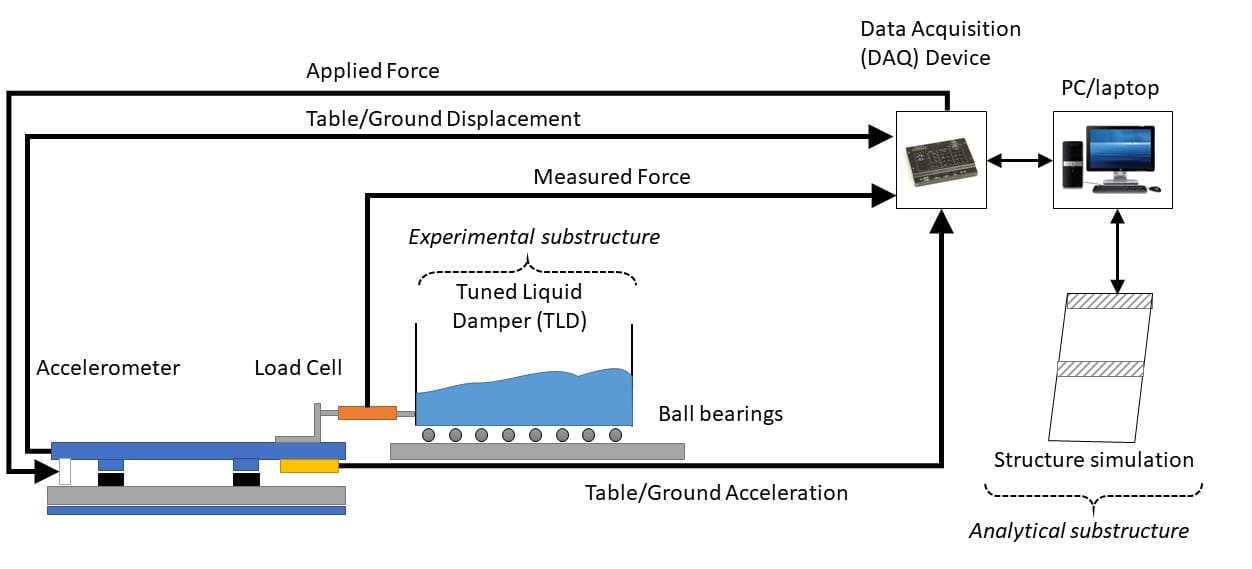
We entered the academic shake table business over 20 years ago. Since then, our Shake Table II and Shake Table III have enabled academics around the globe to conduct cutting edge research in structural dynamics and earthquake engineering. In this blog post, however, I want to focus on one of our lesser talked about products: our classroom-friendly shake table – the Shake Table I-40. In particular, I want to show how you can easily demonstrate a couple of basic structural dynamics concepts in the classroom.
So what is the Shake Table I-40? It is a portable single-axis table capable of creating custom motion profiles (including real earthquake data). With a small footprint, it boasts some impressive specs: a stoke of 40 mm, a resolution of under 2 microns, a maximum accelerating of 1 g, an operational bandwidth of 10 Hz, and an open software architecture. It’s a robust and reliable tool to have around. I personally like the Shake Table I-40 because of its portability; it’s easy to transport and set up in a lab environment or the classroom.
Demo Ideas Using the Shake Table I-40
When it comes to shaking things, our customers have used a variety of structures with the Shake Table I-40, ranging from our own Active Mass Damper (AMD-1) to LEGO blocks to K’Nex structures. My favorite these days is the structural kit produced by a crowdfunded company called Mola. Earlier this year, I ran into Márcio Sequeira, founder, and CEO of Mola at the EERI conference in Vancouver, British Columbia. Márcio took the time to give me a demo, and I bought a Mola Structural Kit I right on the spot knowing that it would be a fantastic companion to our ST I-40.
The kit allows you to quickly build interactive physical models that simulate the static behavior of architectural structures. Throw in a shake table, and you get to analyze structures under dynamic loading. The kit consists of a set of modular parts (bars, rigid connectors, braces, etc.), which are connected through magnets allowing a variety of combinations. You can build different structural systems, visualize the movements and deformations of their elements, and feel the structures using your own hands. It even comes with a cool lab guide!
Natural Frequency
One of the basic characteristics of any dynamic structure is its resonant (or natural) frequency. It’s the frequency at which object like to vibrate in the absence of any external force. Grab yourself a flexible ruler, clamp one end of it on the edge of a table (yes, like a cantilever beam) and flick the other end. That momentary flick will cause the ruler to vibrate at some frequency. Adjust the length of the ruler and flick it again. You’ll notice that it vibrates at a different frequency!
Buildings vibrate in a similar way, well they won’t vibrate when flicked, but they do react to high winds and earthquakes. A building’s natural frequency depends on its stiffness (k) and mass (m) as follows:
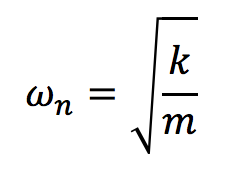
So to alter the natural frequency of a building, one can adjust the building’s mass or frequency. Let’s demonstrate a few of these concepts.
The video below shows a single free-standing column mounted on the shake table. I start by applying a 1 Hz sinusoid to the column, and as you can see, it gently sways back and forth. When I increase the input frequency to 3 Hz, which is around its natural frequency, the bar starts to sway vigorously. Eventually, when I apply an input that is beyond the column’s resonant frequency, e.g., 10 Hz, it hardly moves at all.
Effect of Mass on Natural Frequency
Now let’s look at the effect of mass on the resonant frequency. In the video below, I’ve mounted a short column on the shake table. I’ve estimated that the column has a resonant frequency greater than 10 Hz. Naturally, when I apply a 4 Hz sinusoid, the column hardly shakes. However, when I increase the column’s mass (by adding a round steel ball), I drop its resonant frequency, which causes it to sway more vigorously.
Effect of Stiffness on Natural Frequency
As a final demo, I show how stiffness can alter the natural frequency of a rectangular frame. When I use rigid connectors between the frame components and apply a 5 Hz sinusoid, you can see how noticeably the frame vibrates (pay attention to the mode shape at this frequency). When I stiffen the frame using side bracers (thus increasing its resonant frequency), the structure hardly moves at 5 Hz.
These are all great demos that show basic concepts in structural dynamics. The versatility of the Mola kit combined with the fidelity of our Shake Table I-40 truly brings theory to practice in any structural analysis classroom.